Security and Crypto concepts

Intro

How is our data safe when a lot of it lives in the “cloud”, which is a set of machines we don’t have direct control over. Surely, there must be a way that our data is kept secure so that bad actors don’t have access to it, or it’s in a form that is useless to them even if they get their hand on it.

So in this post, let’s discuss security. Or is it called privacy? What’s the difference anyway? Keep reading if you’re interested.

Disclaimer

I’m not a security expert, so please take this post just as a means to learn the basic building blocks that constitute today’s security infrastructure. There’s a lot of stuff to learn about security, so if you’re building anything serious, I’d highly recommend to do your research and talk to experts.

Terms

Let’s start by defining some common terms.

Security vs Privacy

I’m not at a security expert, so let me quote a description that I liked. It’s taken from here:

“Security and privacy are closely related technologies, however, there are important differences that need to be understood in order to design new systems that address both. Privacy is about informational self-determination–the ability to decide what information about you goes where. Security offers the ability to be confident that those decisions are respected. For example, we talk about GSM voice privacy–can someone listen to my call? There is a privacy goal, which is to allow me to say no, and a security technology, encryption, that allows me to enforce it. In this example, the goals of security and privacy are the same. But there are other times when they may be orthogonal, and there are also times when they are in conflict.”

Another way to think about this is: One can have a very secure app (i.e. have state of the art security systems in place), but at the same time, provide a “feature” that I as a user of the app don’t like because it gives my personal information to people that I don’t want to give my information to.

Privacy, for me, is a basic human right. Things like student grades, medical health records, financial statements, are something that belong to an individual. It’s that individual’s right to decide who to give that information to, if any.

Security, for me, is a technological way to achieve the goal of Privacy. That is, even if app creators have good intentions to make their app private, bad actors can still do things to access data. Security keeps bad actors at bay.

Cryptography

According to this, Crypto (short for Cryptography), is described as:

Cryptography is the practice and study of techniques for secure communication in the presence of third parties called adversaries. More generally, cryptography is about constructing and analyzing protocols that prevent third parties or the public from reading private messages.”

In my mind, it’s not only just about communication but protecting secrets in general. The history of crypto on Wikipedia describes this as:

Cryptography, the use of codes and ciphers to protect secrets, began thousands of years ago.

Crypto is one way to achieve Security.

Website and app functionality generally requires communication between one point (local device) to a remote machine (server). How do you ensure that no one can do something bad if they are able tap on the communication link (network)? Crypto solves that problem.

Once the data is on a server, how do you ensure it’s secured i.e. even if someone gets access to it, it’s useless to them. Crypto solves that problem as well.

Concepts

Entropy

From here:

In information theory, entropy is the measure of uncertainty associated with a random variable. In terms of Cryptography, entropy must be supplied by the cipher for injection into the plaintext of a message so as to neutralise the amount of structure that is present in the unsecure plaintext message. How it is measured depends on the cipher.

Entropy basically is a way to measure the “randomness” of something. It’s units are bits. Let’s say you have \(N\)outcomes of that something. If you’re picking uniformly across these outcomes, the entropy of that something is the the number of bits needed to represent the outcomes, which will be \(\log_2N\).

Let’s discuss a practical example: password strength. A lot of websites today impose constraints on the password you choose. E.g., they’ll ask you to pick certain characters, have a minimum length, etc.

As an example, let’s say you have the following restrictions on your password:

• Length must be at least 7 characters.
• Characters must be in the set {[A-Z], [a-z], [0-9]}. The size of this set is \(26 + 26 + 10 = 62\).

An example of the shortest password you can come up with is: “Test123”.

The entropy of this password is: \(\log_2 (62 ^ 7) \approx 42\) bits. You need as many bits to represent all combinations of a password of length \(7\).

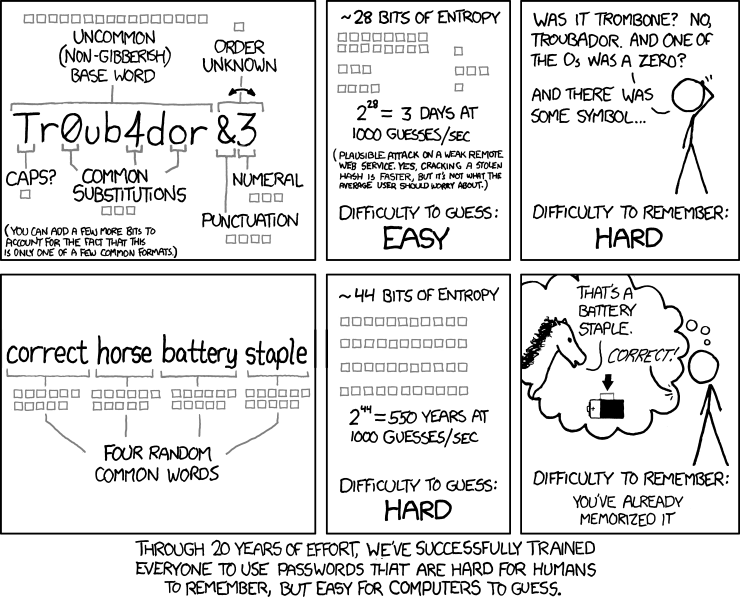
High entropy passwords are harder for computers to crack. That is, the higher the entropy, the harder it is for someone to brute force by guessing all possible outcomes of a password. Practically, there are some practical misconceptions about this though. Here’s a hilarious (but factual) example from xkcd:

Cryptographic hash function

I already defined “function” in one of my other posts.

A cryptographic hash function is a function that takes in an message (input) of arbitrary size, and maps that to a hash value (output) of fixed size. In addition, it must satisfy the following conditions:

1. Must be practically infeasible to invert.
2. Must be deterministic. The same input results in the same hash value. This is actually a general property of a mathematical function i.e. domain:range mapping must be N:1, and never 1:N as discussed here.
3. It is practically infeasible to find two messages that share the same hash value. This is called “collision resistance”.
4. Given a message m1, it’s practical infeasible to find another message m2 that shares the hash value of m1. This is called “target collision resistance”.

Note that “practical infeasibility” is a relative term. For instance, Google found a collision for SHA-1 hash function, thus technically breaking condition #3 above. SHA-1 is a very popular hash function used across the web.

Some other properties of a hash function are:

• It is very fast to compute.
• It generates dissimilar values for similar inputs.

From a programmers point of view, the interface¹ of a hash function is:

1
2
3
4
5

hash(message) -> hash_value
    where
        message := bytearray<arbitrary size>
        hash_value := bytearray<N>
        N := depends on hash function you use

For example, the hash value of a SHA-1 hash function is 160 bits (N = 20 bytes) long. Although, it’s often represented in hexadecimal format (base 16), which means it’ll have 40 hexadecimal digits: \(16^{X} = 2^{160} \implies X = {160\over4} = 40\), where \(X\) is the number of hexadecimal digits.

Git hashes² its commits using SHA-1, although it’s moving to SHA-256.

Let’s see that given a commit, if we can manually recreate the SHA-1 hash value of that commit. For details, you can read this post. I’ve used the same mechanism here.

For this site, here are some commits:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21

$ git log

commit 39d159cb0437c0e1e677380481b33786f162502a (HEAD -> master, origin/master, origin/HEAD)
Author: Syed Paymaan Raza <paymaan.syed@gmail.com>
Date:   Sun Jul 26 17:44:17 2020 -0700

    Enable math in abstractions part 2 post

commit e3bb4537a15cd8844b28dce7e1f0b628785a0d87
Author: Syed Paymaan Raza <paymaan.syed@gmail.com>
Date:   Sun Jul 26 17:07:03 2020 -0700

    Security and Crypto 101 title -> Secruity and Crypto Concepts

commit 5fc44514d8b8c8ce70400d1568ea3cc01b3b18f4
Author: Syed Paymaan Raza <paymaan.syed@gmail.com>
Date:   Sun Jul 26 17:00:32 2020 -0700

    Update README.md
    
    Netlify changes are triggered on Github push, not local commits

Let’s see the content of one of the commits:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

$ git show e3bb4537a15cd8844b28dce7e1f0b628785a0d87
commit e3bb4537a15cd8844b28dce7e1f0b628785a0d87
Author: Syed Paymaan Raza <paymaan.syed@gmail.com>
Date:   Sun Jul 26 17:07:03 2020 -0700

    Security and Crypto 101 title -> Secruity and Crypto Concepts

diff --git a/content/posts/crypto-101.md b/content/posts/crypto-101.md
index 602f9d0..8ae875d 100644
--- a/content/posts/crypto-101.md
+++ b/content/posts/crypto-101.md
@@ -1,5 +1,5 @@
 ---
-title: "Security and Crypto 101 (In progress)"
+title: "Security and Crypto Concepts"
 date: 2020-07-26
 draft: false
 toc: true

Now let’s try to reproduce the commit e3bb4537a15cd8844b28dce7e1f0b628785a0d87 based on the it’s diff content.

Here’s how you do it:

1
2

$ (printf "commit %s\0" $(git cat-file commit e3bb4 | wc -c); git cat-file commit e3bb4) | sha1sum
e3bb4537a15cd8844b28dce7e1f0b628785a0d87  -

Note that we’ve to do some preprocessing before passing the diff content through sha1sum. This is explained here.

Key derivative function

Key derivative functions (or KDFs for short) are a type of crypto hash functions, that among other things, do the following:

1. Are slow to compute. This is intentional so that an attacker can’t brute force by calling the hash function again and again. Depending on the application, this is desirable. We’ll see an example of this later on.
2. Acts as a building blocks for other crypto algorithms by producing “keys” for them. We’ll see an example of this later on.

Symmetric cryptography

Symmetric cryptography is based on a concept of a “key”. The data you want to protect can be “encrypted” using the key, and then “decrypted” using the same key.

This can be thought of as a physical lock. From here:

A symmetric cryptosystem is like a door lock: anyone with the key can lock and unlock it.

From a programmer’s point of view, this is what the interface looks like:

1
2
3
4
5
6

keygen() -> key

encrypt(message: bytearray<any_size>, key) 
    -> encrypted_message: bytearray<any_size>
decrypt(encrypted_message: bytearray<any_size>, key) 
    -> message: bytearray<any_size>

The key here is the shared secret. Anyone who possesses it can know the message. So it’s really important to keep it secure, and not share it with someone who you don’t access to your data.

One common way to generate the key is using a crypto hash function. What will be the input to it, you ask. Well, it can be random based on a property of the computer for example. We’ll see examples of this later.

Two (rather obvious) properties of asymmetric cryptography are:

1. Correctness property i.e. decrypt(encrypt(message, key), key) -> message.
2. It’s practically infeasible to decrypt the encrypted message without the key.

Note that symmetric cryptographic can be used to encrypt data sent over a network, or also encrypt data sitting on a server. Either way, the idea is that if a bad actor gets access to encrypted data, they can’t decrypt it without the key (at least in a practically feasible way).

Asymmetric cryptography

Here, we have two keys; one public which you can share with others, and another private which you must not share. Similar to symmetric cryptography, we can encrypt and decrypt the message (although a bit differently; to be discussed).

This can also be thought of as a physical lock. From here:

Asymmetric encryption is like a padlock with a key. You could give the unlocked lock to someone (the public key), they could put a message in a box and then put the lock on, and after that, only you could open the lock because you kept the key (the private key).

Let’s look at the interface:

1
2
3
4
5
6

keygen() -> (public_key, private_key)

encrypt(message: bytearray<any_size>, public_key) 
    -> encrypted_message: bytearray<any_size>
decrypt(encrypted_message: bytearray<any_size>, private_key) 
    -> message: bytearray<any_size>

In addition to the above, asymmetric has some other nice interfaces around “signature” and “verification”:

1
2
3
4

sign(message: bytearray<any_size>, private_key) 
    -> signature: bytearray<any_size>
verify(message: bytearray<any_size>, signature: bytearray<any_size>, public_key) 
    -> True/False

“sign” and “verify” have these properties:

1. It’s practically infeasible to forge a signature without the private key. In other words, without a private key, you can’t find a signature for which verify(message, signature, public_key) returns True.
2. Correctness property: verify(message, sign(message, private key), public key) = True.

So now you might ask, what’s the benefit of having two separate keys (public and private)? The main reason is:

• By sharing the public key you allow anyone to encrypt stuff and send to you, which then you can only decrypt. That’s not possible in symmetric crypto model. “sign” and “verify” also work the same way.

Case studies

If you are interested, you can now apply these principles and learn about practical use-cases:

• Passwords (login screens, password managers, storing password credentials). Also understand why passwords are salted.
• 2FA (yubikey)
• Encryption (disk, cloud, pgp email)
• SSH
• Private messaging (signal, keybase)
• Git. Note that git hashes commits for correctness, not security. Learn about gpg signed commits for security.
• Commitment schemes (why people on twitter tweet hashes and later show original content).
• Software mirror verification
• Website authentication (OAuth tokens)
• HTTPS, SSL
• Key distribution. Challenge in asymmetric crypto: How to map public key to real life identity? Same concept as “blue checkbox” in Twitter. Different models.

If you have more time, learn about the differences of these commonly used terms:

• Authentication vs Authorization
• Encoding vs Decoding
• Encrypting vs Decrypting

References

A lot of the content in this post was inspired from MIT’s excellent Missing Semester course’s lecture on Security.